Supplément 4.8: Expérience sur la diffusion par l'eau

Diffusion par l'eau, un exemple de diffusion de Rayleigh

Le coefficient d'absorption de l'eau liquide est inférieur à 1/m pour toutes les longueurs d'onde visibles. Dans la gamme des bleus, l'eau est particulièrement transparente, le coefficient d'absorption y est d'environ 0,02/m.

Le coefficient de diffusion de l'eau est inférieur d'un facteur 10 dans la zone bleue. Cela est dû à la petite taille de la molécule par rapport à la longueur d'onde de la lumière : son diamètre est d'environ 2 Å ou 2·10^-10 m (l'Ångström, avec le signe d'unité Å, est une unité de longueur courante en physique atomique). Les molécules d'eau sont donc un exemple de particules caractérisées par la diffusion de Rayleigh.

Nous étudions ici comment un échantillon d'eau diffuse la lumière d'un laser.

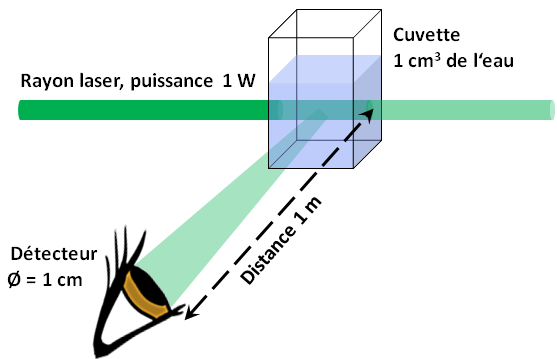
L'installation expérimentale

Une cuvette remplie d'eau est éclairée par un faisceau laser bleu-vert. La longueur d'onde est de 500 nm, la puissance de rayonnement est de 1 W (si vous souhaitez reproduire l'expérience : ce laser n'est en aucun cas sans danger pour les yeux, veuillez faire preuve d'une extrême prudence).

A 90° par rapport à la direction du faisceau laser, nous observons d'abord à l'œil nu la lumière diffusée produite sur l'eau. Soit un volume d'eau éclairé et visible de V = 1 cm³.

Montage expérimental pour la mesure de la diffusion de la lumière à partir d'un échantillon d'eau.
Source: Rainer Reuter, Université d'Oldenburg, Allemagne.

Nous fixons ensuite une photodiode pour une mesure quantitative à une distance de r = 1 m de la cuvette et également à 90°. Le diamètre de la zone photosensible est d = 1 cm. A 500 nm, on admet que la sensibilité de la photodiode, c'est-à-dire le photocourant (en ampères) de la diode généré par une puissance optique (en watts), est de S = 0,5 A/W.

Propriétés de diffusion de l'eau

Les très petites particules diffusent la lumière de manière symétrique dans les demi-espaces avant et arrière. Ce phénomène est caractéristique de la diffusion de Rayleigh des petites particules. Si l'angle de diffusion mesuré par rapport à la direction du faisceau laser est noté θ, la fonction de diffusion de la lumière non polarisée est donnée par l'équation suivante

β (θ) = β (90 °) (1 + {cos}^{2} θ)

Diagramme polaire de la fonction de phase en fonction de l'angle θ pour des particules de diamètre 2 Å, d'indice de réfraction n = 1,33 et pour une lumière de longueur d'onde 500 nm. La fonction de phase est égale à la fonction de diffusion β divisée par le coefficient de diffusion b. Nous calculerons la valeur de b dans la colonne de droite.
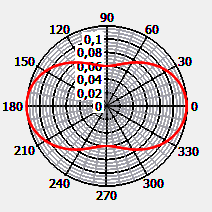
Créé avec MieSimulatorGUI, Version 1.3, dernier accès : 30 mars 2023.

La valeur bibliographique de la fonction de diffusion pour un angle de diffusion de 90° à la longueur d'onde 500 nm est la suivante (Zhang & Hu, 2021) :

β (90 °) = 1,38 \cdot 10^{- 4} \frac{1}{m sr}

Equations ↓

La masse molaire de l'eau est d'environ 18 g, ce qui correspond à un volume molaire d'environ 18 cm³. Le nombre de particules dans la mole est donné par la constante d'Avogadro 6·10²³. Le nombre de molécules d'eau dans 1 m³ est donc :

N = \frac{6 \cdot 10^{23}}{18 \cdot 10^{- 6} m^{3}} = 3,3 \cdot 10^{28} \frac{1}{m^{3}}

La section efficace différentielle de la diffusion à 90° se traduit par :

σ (90 °) = \frac{β (90 °)}{N} = 4,14 \cdot 10^{- 33} \frac{m^{2}}{sr}

La luminosité au niveau de l'œil

L'intensité de la lumière diffusée découle des valeurs de la fonction de diffusion β de l'eau et de l'irradiance E du laser sur le volume d'eau éclairé V, selon la formule suivante

I = β E V

où E = 1 W/cm² et V = 1 cm³. La puissance optique au niveau de l'œil ou du détecteur résulte de cette intensité multipliée par l'angle solide Ω auquel l'œil ou le détecteur apparaît vu de l'eau diffusante :

P = I (90 °) Ω = β (90 °) E V \frac{π d^{2} / 4}{r^{2}}

En remplaçant toutes les valeurs, on obtient la puissance optique P ≈ 10^-10 W ou 0,1 nanowatt. L'œil peut-il encore voir cela ?

Pour répondre à cette question, il est utile de revenir à l'image photonique de la lumière. Un œil adapté à l'obscurité peut percevoir environ un photon sur 50 qui frappe la rétine comme un faible éclair de lumière. Pour la lumière monochromatique, la relation entre la puissance optique et le nombre de photons correspondant est la suivante :

P = N_{P h o t o n} E_{P h o t o n}

où N_Photon est le nombre de photons par seconde et l'énergie des photons E_Photon = hc/λ. h est la constante de Planck et et c la vitesse de la lumière. Il s'ensuit que N_Photon ≈ 250· 10⁶ ou 250 millions de photons par seconde.

Le signal du détecteur

Le photocourant de la photodiode résulte de la puissance optique incidente et de sa sensibilité, qui a été supposée être S = 0,5 A/W ci-dessus. Il s'agit donc de

I_{p h o t o} = S P = 0,5 \cdot 10^{- 10} A

ou 50 picoampères. Les multimètres électriques n'atteignent au mieux que la gamme des microampères, c'est pourquoi vous avez besoin d'un ampèremètre beaucoup plus sensible. Ces appareils sont appelés picoampèremètres.

Le coefficient de diffusion

Si la fonction de diffusion est intégrée sur l'ensemble de l'espace, on obtient le coefficient de diffusion :

\begin{array}{l} b = \int_{Ω = 4 π} β d Ω = 2 π \int_{θ = 0}^{π} β (θ) sin θ d θ \\ = 2 π β (90 °) \int_{θ = 0}^{π} (1 + {cos}^{2} θ) sin θ d θ = 16 \frac{π}{3} β (90 °) \end{array}

L'insertion donne : $b = 2,3 \cdot 10^{- 3} /m$

Sur une distance de 1 m, le faisceau laser perd 2,3 pour mille de sa luminosité en raison de la diffusion. La diminution de luminosité dans la cuvette de notre expérience, qui ne mesure qu'un centimètre de long, est pratiquement négligeable.

La section efficace de diffusion totale (intégrée sur l'ensemble de l'espace) devient :

σ = \frac{b}{N} = 7 \cdot 10^{- 32} m^{2}

Par rapport à leur section géométrique, les molécules n'occultent donc qu'une très petite partie de la luminosité du faisceau laser.

En fait, la diffusion de la lumière par l'eau est influencée par d'autres variables. La température, la pression et, dans le cas de l'eau de mer, la salinité jouent un rôle. De plus, des fluctuations de densité se produisent dans le liquide, ce qui contribue également à la diffusion. La publication de Zhang & Hu, 2021 fournit des informations détaillées à ce sujet.